TBY's Blog

相关矩阵的求解的一些优化心得

问题如下，有 $n \times m$ Matrix, where $n > 10^4$ , $m$ ～ $100$ ，以Row-major order 存储于内存中，需要求相关矩阵 $M_{cor}$ 。由于相关矩阵是对称的，所以只需要求上半个矩阵，共 $p = \frac{(n-1)n}{2}$ 次相关系数求解。求解计算本身很简单无外乎：

for(int i=0;i<r;i++)
  for(int j=i+1;j<r;j++)
  {
    double r = correlation(row(i),row(j));
  }

现在想并发该计算，考虑cache locality，最理想的并发方式无疑是顺序产生如下[(i,j)序列：

1	`(0,1),(0,2),(0,3) ... (1,2),(1,3) ... (2,3),(2,4) ...`

然后再以如下方式并发(以4核为例):

// thread 1 :
for (int idx = 0; idx < (n-1)*n/2; idx=idx+4) {
   (i,j) = calc(idx);
   double r1 = correlation(row(i),row(j));
}
 
// thread 2 :
for (int idx = 1; idx < (n-1)*n/2; idx=idx+4) {
   (i,j) = calc(idx);
   double r2 = correlation(row(i),row(j));
}
 
// thread 3 :
for (int idx = 2; idx < (n-1)*n/2; idx=idx+4) {
   (i,j) = calc(idx);
   double r3 = correlation(row(i),row(j));
}
 
// thread 4 :
for (int idx = 3; idx < (n-1)*n/2; idx=idx+4) {
   (i,j) = calc(p);
   double r4 = correlation(row(i),row(j));
}

好了，所以重点在于如何以并不高的代价解出那个calc函数。想了一下，直接要 idx -> (i,j) 不太容易，先反过来如何从(i,j) -> idx，草稿纸推了下（我小学数学老师要哭了，推了蛮长时间），idx满足以下等式：

$idx = \frac{n\times(n-1)-(n-i-1)\times(n-i)}{2}+j-i-1=\frac{2\times i\times n-i^2-3i+2j-2}{2}$

这个关系蛮容易验证的：

test.c
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	`#include <stdio.h>` `int` `main(int` `argc,` `char` `argv[])` `{` `int` `n = 10;` `int` `i,j;` `int` `idx = 0;` `for(i=0;i<n;i++)` `for(j=i+1;j<n;j++)` `{` `int` `p = (n(n-1) - (n-1-i)(n-i))/2 + j - i - 1;` `int` `q = (2 i * n - i * i - 3 * i + 2 * j - 2) / 2;` `printf("%d %d %d\n",p,q,idx);` `++idx;` `}` `return` `0;` `}`

有了上述关系式子以后，可以发现，事实上，原先要求解的calc可以用一个整形规划来描述:

$idx = \frac{2\times i\times n - i^2 -3i +2j-2}{2}$ ，subject to :

$0 \le i < n, i < j < n, 0 \le idx < \frac{(n-1)n}{2}$ ，其中i,j,n,idx皆为整数。

这里当然不可能用通用的整形规划相关的库(比如glpk),去解这种小儿科问题。看看有无其他办法。下面代码直接都上Haskell了，C之类太繁琐，写一小段代码都得撸半天。由关系式可以得到一个判别式:

1 2	`testIdx ::` `Int` `->` `Int` `->` `Int` `->` `Bool` `testIdx i j idx = (2in-ii-3i+2j-2) == idx ` `2`

所以可以穷举所有i、j的可能值来求得idx:

f1 :: Int -> Int -> (Int,Int)
f1 n idx = head [(i,j) | i <- [0..n-2], 
                         j <- [i+1..n-1],
                         testIdx i j idx]

当然，这是个很笨的办法，当 n > 1000时已经很慢了。进一步优化需要利用那些约束，由于(i,j)都属于上三角阵的元素，所以很自然的想法就是去缓存那些 边界条件 (其实求解整形规划问题也就是这路子)，在这里就是对角线上那一排(i,j)对应的idx值。这个比较容易，因为那些点还有个隐含关系： $j = i + 1$ 。

f2 :: Int -> Int -> (Int,Int)
f2 n idx = -- quot开销比div更小, Haskell中的div比quot多额外的检查项，这里都是正整数运算无此必要
  let i = getI idx
      j = getJ i idx
  in (i,j)
  where
    getJ :: Int -> Int -> Int
    getJ i p = (2*p+i*i+3*i-2*i*n+2) `quot` 2
    getI :: Int -> Int
    getI ix = length (takeWhile (<= ix) ps0) - 1
    ps0 :: [Int] -- 上对角元素对应的idx值
    ps0 = map (\i -> (2*i*n-i*i-i) `quot` 2) [0..n-2]

上面f2在n=100时，比f1快了4.5倍，但还是不够高效，因为每次求解还是要重新计算ps0，所以很自然的想法就是再把ps0拉出来缓存。

import qualified Data.Vector.Unboxed as UV
getVec :: Int -> UV.Vector Int
getVec n = UV.generate n (\i -> (2*i*n-i*i-i) `quot` 2)  
 
            
f3 :: UV.Vector Int -> Int -> (Int,Int)
f3 vec idx =
  let i = getI
      j = getJ i
  in (i,j)
  where
    n = UV.length vec
    getJ i = (2*idx+i*i+3*i-2*i*n+2) `quot` 2
    getI = go 0
      where
        go acc | acc == n - 1 = acc
               | otherwise = if UV.unsafeIndex vec  (acc+1) > idx
                             then acc
                             else go (acc+1)

略微修改上述f1，f2，f3以便同时测试程序正确性，得到如下benchmark.hs文件

benchmark.hs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63	`import` `Criterion.Main` `import` `qualified` `Data.Vector.Unboxed` `as` `UV` `f1 ::` `Int` `->` `Bool` `f1 n =` `let` `l = (n * (n-1`)) ``quot`` `2` `ls = [0..l-1]` `in` `and` `$` `zipWith` `(==) ls $` `map` `(\p ->` `head` `[getP i j \| i <- [0..n-2],j <- [i+1..n-1],testP i j p]) ls` `where` `testP ::` `Int` `->` `Int` `->` `Int` `->` `Bool` `testP i j p = (2in-ii-3i+2j-2) == p ` `2` `getP ::` `Int` `->` `Int` `->` `Int` `getP i j = (2in-ii-3i+2j-2`) ``quot`` `2` `f2 ::` `Int` `->` `Bool` `f2 n =` `let` `l = (n (n-1`)) ``quot`` `2` `ls = [0..l-1]` `in` `and` `$` `zipWith` `(\a b -> a == b) ls $` `map` `(\p ->` `let` `i = (length` `$` `takeWhile` `(<= p) ps0) -` `1` `j = getJ i p` `in` `getP i j) ls` `where` `getP ::` `Int` `->` `Int` `->` `Int` `getP i j = (2in-ii-3i+2j-2`) ``quot`` `2` `getJ ::` `Int` `->` `Int` `->` `Int` `getJ i p = (2p+ii+3i-2in+2`) ``quot`` `2` `ps0 :: [Int]` `ps0 =` `map` `(\i -> (2`in-ii-i) ``quot`` `2) [0..n-2]` `f3 :: UV.Vector` `Int` `->` `Int` `->` `Bool` `f3 vec n =` `let` `l = (n (n-1`)) ``quot`` `2` `ls = [0..l-1]` `in` `and` `$` `zipWith` `(==) ls $` `map` `(\p ->` `let` `i = getIdx p` `j = getJ i p` `in` `getP i j) ls` `where` `getP i j = (2in-ii-3i+2j-2`) ``quot`` `2` `getJ i p = (2p+ii+3i-2in+2`) ``quot`` `2` `getIdx p = go` `0` `where` `go acc \| acc == n -` `1` `= acc` `\|` `otherwise` `=` `if` `UV.unsafeIndex vec (acc+1) > p` `then` `acc` `else` `go (acc+1)` `main =` `do` `let` `vec = getVec` `100` `print` `$ f1` `100` `print` `$ f2` `100` `print` `$ f3 vec` `100` `defaultMain` `[bench` `"f1 100"` `$ nf f1` `100` `,bench` `"f2 100"` `$ nf f2` `100` `,bench` `"f3 100"` `$ nf (f3 vec)` `100` `,bench` `"f3 1000"` `$ nf (f3 (getVec` `1000))` `1000]`

结果：

benchmark.hs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38	`$ ghc --make` `-O2 -fllvm -optl-O3 benchmark.hs` `$ ./benchmark` `True` `True` `True` `warming up` `estimating clock resolution...` `mean is 1.296372 us (640001 iterations)` `found 3334 outliers among 639999 samples (0.5%)` `3075 (0.5%) high severe` `estimating cost of a clock call...` `mean is 35.00575 ns (12 iterations)` `benchmarking f1 100` `mean: 13.92723 ms, lb 13.88566 ms, ub 13.96976 ms, ci 0.950` `std dev: 215.6054 us, lb 190.5129 us, ub 246.8802 us, ci 0.950` `variance introduced by outliers: 8.472%` `variance is slightly inflated by outliers` `benchmarking f2 100` `mean: 2.810448 ms, lb 2.801007 ms, ub 2.821439 ms, ci 0.950` `std dev: 52.27388 us, lb 43.98545 us, ub 65.98971 us, ci 0.950` `found 3 outliers among 100 samples (3.0%)` `3 (3.0%) high mild` `variance introduced by outliers: 11.350%` `variance is moderately inflated by outliers` `benchmarking f3 100` `mean: 173.9339 us, lb 173.4058 us, ub 174.5147 us, ci 0.950` `std dev: 2.829666 us, lb 2.432605 us, ub 3.579531 us, ci 0.950` `found 2 outliers among 100 samples (2.0%)` `2 (2.0%) high mild` `variance introduced by outliers: 9.410%` `variance is slightly inflated by outliers` `benchmarking f3 1000` `mean: 17.29405 ms, lb 17.26062 ms, ub 17.33314 ms, ci 0.950` `std dev: 185.0009 us, lb 157.9185 us, ub 221.9862 us, ci 0.950`

后记：实际运算的时候，其实并不需要像上面那样给定任意idx求其(i,j)，因为i总是从0起始迭代的，所以只需要用关系式求j，并判定下是否需要更新i即可。运算量非常小。

Diagrams画直方图————Plot补完计划（一）

这是个蛋疼系列，计划用Diagrams实现所有常用的统计绘图，目的主要是扩充自己的工具箱，绘图时能够摆脱外部的统计软件，并且能根据实际数据需要，方便地自定义修改。代码风格的话，属于想到啥写啥，不会太严谨。

用Diagrams画过一些矢量图以后，发现真正麻烦的地方不是“图形”本身，而是字体、数轴、缩放比例，这些琐碎的东西反而会占据90%以上的代码。以直方图为例，图形本身很简单，差不多1～2行能搞定（第18、19行）。

简单直方图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32	`import` `Data.Colour` `import` `Data.Colour.Names` `import` `qualified` `Data.Vector.Generic` `as` `GV` `import` `qualified` `Data.Vector.Unboxed` `as` `UV` `import` `Diagrams.Backend.Cairo.CmdLine` `import` `Diagrams.Prelude` `import` `Statistics.Distribution` `import` `Statistics.Distribution.Normal` `import` `qualified` `Statistics.Sample.Histogram` `as` `H` `import` `System.Random.MWC` `import` `qualified` `System.Random.MWC.Distributions` `as` `R` `import` `Text.Printf` `histogram nBin c vec =` `let` `(low,up) = H.range nBin vec` `w = (up - low) /` `fromIntegral` `nBin` `v = H.histogram_ nBin low up vec :: UV.Vector` `Double` `his = alignBL . hcat .` `map` `(safeRect w) . GV.toList $ v -- 直方图` `maxH = UV.maximum` `v` `factorX = maxH / (ratio * (up - low)) -- ratio,图最后的宽：高的比例` `fontS = maxH /` `20` `-- 字体大小` `in` `(yAxis maxH fontS \|\|\| strutX (fontS/2) \|\|\|` `(his # scaleX factorX === strutY (fontS/2) ===` `xAxis low up fontS factorX))` `# centerXY` `where` `safeRect w h =` `if` `h /=` `0` `--` `0.6版本rect函数，h==0时会报错` `then` `rect w h` `# alignB` `# fcA c` `else` `hrule w` `# alignB`

麻烦的地方开始了，你需要图形的数轴自动标上合适的Label吧，需要图形能自动根据自身的长宽比选择一个合适的缩放比例吧。我发现下面这个unit函数可以比较好的自动选择数轴单位，不会使ticks太密集或者稀疏。fmtStr是和printf配合使用，选择一个合适的数字格式。如此，数轴的其他部分绘制基本就无难度了。

unit :: (Ord a,Floating a) => a -> a -> a
unit low up = last $
              takeWhile (\c -> (up - low) / c >= 4.5) $
              takeWhile (<= (up - low)) $
              concatMap (\c ->  map (10^^c *) [1,2,5])  ([-4..]::[Int])
{-# INLINABLE unit #-}
 
fmtStr low up | up - low >= 5 = "%.0f"
              | up - low >= 0.5 = "%.1f"
              | up - low >= 0.25 = "%.2f"
              | up - low >= 0.125 = "%.3f"
              | otherwise = error "too small interval"

因为实际应用的时候，往往会用数据做个期望最大化估计，得到一个理论分布的概率密度函数来做比较，可以再在histogram函数上略做修改，添加绘制概率密度函数的代码部分。这块麻烦的地方主要在于计算概率密度函数的缩放比例。

histogram' nBin (vec,c) (d,c') = -- d : Statistics.Distribution中的Distribution
  let (low,up) = H.range nBin vec
      w = (up - low) / fromIntegral nBin
      v = H.histogram_ nBin low up vec ::  UV.Vector Double
      n = fromIntegral $ GV.length vec
      his = alignBL . hcat . map (safeRect w) . GV.toList $ v
      ls = [low,low+w/2..up]
      maxH = UV.maximum v
      factorX = maxH / (ratio * (up - low))
      fontS = maxH / 20
      vs = fromVertices $ map p2 $ zip ls $ map ((f *) . (density d)) ls
      f = w * n / (cumulative d up - cumulative d low) -- 总面积 / cdf跨过的面积
      funP = vs # stroke # lw (fontS/10) # lcA c' # moveOriginTo (p2 (low,f*(density d low))) -- 与直方图的原点对齐
  in (yAxis maxH fontS ||| strutX (fontS/2) |||
      ((funP <> his) # scaleX factorX === strutY (fontS/2) ===
       xAxis low up fontS factorX))
     # centerXY
  where
    safeRect w h = if h /= 0
                   then rect w h
                        # alignB
                        # fcA c
                   else hrule w
                        # alignB

绘制效果：

所有代码如下：

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

{-# LANGUAGE NoMonomorphismRestriction #-}
{-# OPTIONS_GHC -fno-warn-missing-signatures #-}
-----------------------------------------------------------------------------
-- |
-- Module : 一些柱状图相关便利函数
-- Copyright : (c) 2012 Boyun Tang
-- License : BSD-style
-- Maintainer : tangboyun@hotmail.com
-- Stability : experimental
-- Portability : ghc
--
-- 
--
-----------------------------------------------------------------------------
module Main where
 
import           Data.Colour
import           Data.Colour.Names
import qualified Data.Vector.Generic as GV
import qualified Data.Vector.Unboxed as UV
import           Diagrams.Backend.Cairo.CmdLine
import           Diagrams.Prelude
import           Statistics.Distribution
import           Statistics.Distribution.Normal
import qualified Statistics.Sample.Histogram as H
import           System.Random.MWC
import qualified System.Random.MWC.Distributions as R
import           Text.Printf
 
ratio = (sqrt 5 - 1) / 2
 
histogram' nBin (vec,c) (d,c') =
  let (low,up) = H.range nBin vec
      w = (up - low) / fromIntegral nBin
      v = H.histogram_ nBin low up vec ::  UV.Vector Double
      n = fromIntegral $ GV.length vec
      his = alignBL . hcat . map (safeRect w) . GV.toList $ v
      ls = [low,low+w/2..up]
      maxH = UV.maximum v
      factorX = maxH / (ratio * (up - low))
      fontS = maxH / 20
      vs = fromVertices $ map p2 $ zip ls $ map ((f *) . (density d)) ls
      f = w * n / (cumulative d up - cumulative d low)
      funP = vs # stroke # lw (fontS/10) # lcA c' # moveOriginTo (p2 (low,f*(density d low)))
  in (yAxis maxH fontS ||| strutX (fontS/2) |||
      ((funP <> his) # scaleX factorX === strutY (fontS/2) ===
       xAxis low up fontS factorX))
     # centerXY
  where
    safeRect w h = if h /= 0
                   then rect w h
                        # alignB
                        # fcA c
                   else hrule w
                        # alignB
 
 
histogram nBin c vec =
  let (low,up) = H.range nBin vec
      w = (up - low) / fromIntegral nBin
      v = H.histogram_ nBin low up vec ::  UV.Vector Double
      his = alignBL . hcat . map (safeRect w) . GV.toList $ v -- 直方图
      maxH = UV.maximum v
      factorX = maxH / (ratio * (up - low)) -- ratio,图最后的宽：高的比例
      fontS = maxH / 20 -- 字体大小
  in (yAxis maxH fontS ||| strutX (fontS/2) |||
      (his # scaleX factorX === strutY (fontS/2) ===
       xAxis low up fontS factorX))
     # centerXY
  where
    safeRect w h = if h /= 0 -- 0.6版本rect函数，h==0时会报错
                   then rect w h
                        # alignB
                        # fcA c
                   else hrule w
                        # alignB
 
xAxis low up fSize factorX =
  let ls = takeWhile (<= len) [beginAt,beginAt + step..]
      beg = fromIntegral $ (ceiling low :: Int)
      ls' = take (length ls) [beg,beg+step..]
      len = up - low
      step = unit low up
      beginAt = beg - low 
      fmt = fmtStr beginAt (last ls) 
      ticks = map (\l ->
                    alignT $
                    (vrule (fSize/3) # lw (fSize/20) === strutY (fSize/2) ===
                     text' fSize (printf fmt l))
                  ) ls' 
      vs = map p2 $ zip (map (* factorX) ls) (repeat 0)
  in (hrule len # lw (fSize / 10) # alignL) # scaleX factorX <>
     position (zip vs ticks)
 
yAxis maxH fSize =
  let step = unit 0 maxH
      ls = takeWhile (<= maxH) [step,step+step..]
      fmt = fmtStr step (last ls)
      vs = map p2 $ zip (repeat 0) ls
      ticks = map (\l ->
                    alignR $
                    (text' fSize (printf fmt l) ||| strutX (fSize/2) |||
                     hrule (fSize/3) # lw (fSize/20))
                  ) ls
  in vrule maxH # lw (fSize / 10) # alignB <>
     position (zip vs ticks)
      
      
text' h t = text t # fontSize h <> rect (fromIntegral (length t) * 0.6 * h) h # lcA transparent
 
unit :: (Ord a,Floating a) => a -> a -> a
unit low up = last $
              takeWhile (\c -> (up - low) / c >= 4.5) $
              takeWhile (<= (up - low)) $
              concatMap (\c ->  map (10^^c *) [1,2,5])  ([-4..]::[Int])
{-# INLINABLE unit #-}
 
fmtStr low up | up - low >= 5 = "%.0f"
              | up - low >= 0.5 = "%.1f"
              | up - low >= 0.25 = "%.2f"
              | up - low >= 0.125 = "%.3f"
              | otherwise = error "too small interval"
 
main = do
  gen <- create
  randVec <- UV.replicateM 100000 (R.standard gen)
  defaultMain $ do
    histogram' 100 (randVec,blue `withOpacity` 0.8) (normalFromSample randVec, green `withOpacity` 0.8)
         
        

后记：Statistics.Sample.Histogram中的两个histogram函数接口不是很好用，如果只画一层直方图无疑是足够的，但是统计绘图里有时候需要绘制2层直方图（比如实际数据一层、permutation test产生的一层，再加上个经验贝叶斯估计的函数，如下图），它的接口两套数据无法共用一个bin。。。还不如自己写。。。Diagrams目前最大的软肋还是字体处理，这点上估计是没希望超越LaTeX+pgfplots的，下图的其他效果都容易做到，唯独数学字体。。。。。

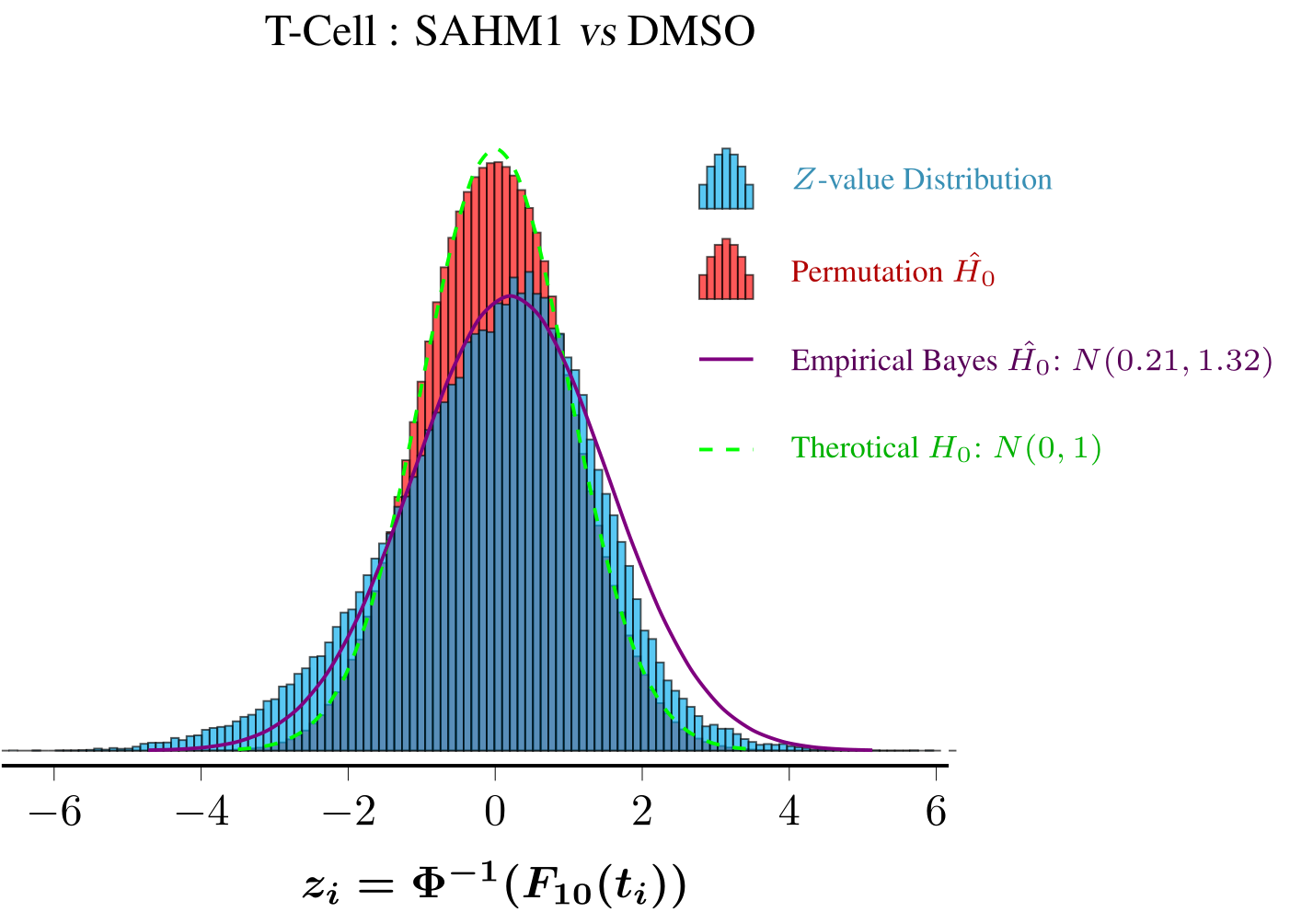
数据展示与Diagrams库

因为做的是一些数据分析相关的工作，对数据展示格外感兴趣，所以一直在尝试寻找一些好用的低层矢量图形函数库。

尝试过各类数值软件、LaTex的tikz和pgfplots包等。高级的绘图API无疑用起来很方便，但相应的可定制性就较差。tikz和pgfplots是我之前最喜欢用的，不过坏在LaTeX不是个好用的数值软件。之前用Haskell的StringTemplate包写过一个绘制约3w多个点的tex文件，这时候直接用LaTeX编译会爆内存的(LuaLaTeX OK)。用tikz和pgfplots之类的宏包，最强的地方在于完美的数学字体，这方面我仍未发现不通过调用LaTeX能达到相应效果的库。传统的cairo无疑是个很棒的矢量图库，不过太底层，无法想象用裸API能够快速开发。

Haskell的diagrams库，也就是在这里要介绍的，是个很有Haskell风格(各种combinator)的矢量图形库，尝试了一番以后，我非常满意，考虑以后大部分图形函数都移到这库上来。优点主要有以下几点：

图是“拼”出来的,而不是传统的一笔一划“画”出来的。
后端很丰富，可以导出位图（bmp、png）、矢量(svg、ps、pdf）和tex文件(tikz后端)。
表现力很强，语言（DSL）本身很抽象，API设计的也很合理。
diagrams-core令人惊讶地简洁。

这里就举几个生物上的例子。最近在弄一些microRNA靶基因预测方面的算法，一个预测的靶点好坏，其实可以很直观的看出来的：

Seed Match的类型（miRNA 5'端的第2～7号碱基与靶的互补情况, 1 based）
3’端特定位置的氢键数量
Seed序列周围的A或U碱基含量百分比
靶点的结合区在基因3'UTR区的相对位置。
一个比较promising的预测位点应该在不同物种中趋向于保守。

网上的数据库为了展示方便，往往只用文本来展示这类信息，非常不幸的是，如果你没有在浏览器中设置等宽字体，打开我给的那个链接时，你很难直观地看出这些信息。这里“对齐”和“颜色设置”对于良好地展示数据非常重要。

上面这两块svg便是用diagrams绘制的，代码其实很简单（主要琐碎在计算下标和颜色设置上），诀窍是在需要对齐的部分，把字符当块来处理对齐。

代码示例
1 2 3 4 5 6 7 8 9 10 11	`-- \| 黑白字母` `char ch = text [ch] <>` `rect w h # lcA transparent` `-- \| 彩色字母` `charC c ch = text [ch] # fc c <>` `rect w h # lcA transparent` `-- \| 下面是相应的字串` `string = hcat .` `map` `char` `stringC c = hcat .` `map` `(charC c)`

想了解microRNA的可以看看下面的文献。另：TargetScan的预测算法在已知结合位置的情况下是相当简单的，大约只有半小时的编程量。

Most Mammalian mRNAs Are Conserved Targets of MicroRNAs
Robin C Friedman, Kyle Kai-How Farh, Christopher B Burge, David P Bartel. Genome Research, 19:92-105 (2009).

简单的图片去背景

上传头像时，想弄个透明背景。图片本身背景很单一，但gimp扣了下发现魔棒效果很差，无法与PS相比。

用Haskell随手写了个小东西，根据亮度来降alpha通道值。一开始还想弄个复杂点的阈值函数，调了几下，发现简单的才是最好的。

修改Alpha通道
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22	`module` `Main` `where` `import` `System.Environment` `import` `Codec.Picture` `main =` `fmap` `head` `getArgs >>= readPng >>=` `writePng` `"out.png"` `.` `(\(Right` `(ImageRGBA8 im)) ->` `pixelMap` `(\(PixelRGBA8 r g b al) ->` `let` `a = (fromIntegral` `r) +` `(fromIntegral` `g) +` `(fromIntegral` `b) ::` `Int` `alpha =` `if` `a > (` `3` `` `245)` `then` `0` `else` `if` `a > (3200)` `then` `round` `$` `(fromIntegral` `(a - (3200)) /` `fromIntegral` `((3255)::Int)) *` `255` `else` `al` `in` `PixelRGBA8 r g b alpha) im)`